Continuidad. Teoremas.
Profesor David Sánchez Ortiz | www.davidso.es | contacto@davidso.es
¿Cuándo decimos que una función \( f(x) \) es continua en \( x_0 \) ?
- Existe la imagen \( f(x_0) \)
- Existe el límite \( \displaystyle \lim_{x\to x_0}{f(x)}\) y es finito
- Se cumple que \( f(x_0) = \displaystyle \lim_{x\to x_0}{f(x)} \) o lo que es lo mismo, la imagen y el límite coinciden.
Si alguna de estas condiciones falla, diremos que hay una discontinuidad en \( x_0 \) y la clasificaremos de la siguiente manera:
🔵 1. Discontinuidad evitable
Ocurre cuando el límite existe y es finito, pero:
- La función no está definida en ese punto.
- O está definida, pero \( f(x_0) \ne \lim f(x) \)
Podríamos “arreglarla” redefiniendo la función en ese punto. Por eso se llama evitable.
🔴 2. Discontinuidad de primera especie de salto finito
Los límites laterales existen y son finitos, pero no coinciden.
Ejemplo típico: funciones a trozos con valores diferentes a izquierda y derecha de un punto.
⚠️ 3. Discontinuidad de primera especie de salto infinito
Alguno de los límites laterales tiende a infinito. Suele aparecer en funciones racionales con asíntotas verticales.
🟣 4. Discontinuidad esencial o de segunda especie
Al menos uno de los límites laterales no existe como por ejemplo que el límite no exista porque hay raíz o logaritmo de número negativo o porque la función no está definida a un lado del punto frontera.
No confundas: Que el límite tienda a infinito 👉 sí existe (infinito)
🎓 Resumen de continuidad:
- ✅ Continua: \( f(x_0) \) existe, el límite también, y coinciden.
- 🚫 Evitable: el límite existe pero \( f(x_0) \) no coincide o no está definida.
- ↕️ Salto finito: límites laterales finitos pero diferentes.
- ∞ Salto infinito: uno o ambos límites tienden a \( \infty \).
- ❓ Esencial: algunos de los límites laterales no existen.
Teoremas relativos a la continuidad
Teorema de conservación del signo.
Si una función continua no se anula en un intervalo cerrado \( [a, b] \), entonces mantiene el mismo signo en todo ese intervalo.
Es decir, si \( f(x) \neq 0 \) para todo \( x \in [a, b] \), entonces:
- o bien \( f(x) > 0 \) en todo el intervalo,
- o bien \( f(x) < 0 \) en todo el intervalo.
✅ Esto permite garantizar que una función continua que es positiva (o negativa) al inicio de un tramo y nunca se anula, lo será en todo el intervalo.
Teorema de Bolzano.
Si una función continua en un intervalo cerrado \( [a, b] \) toma valores de distinto signo en los extremos, entonces existe al menos un punto \( c \in (a, b) \) tal que \( f(c) = 0 \).
Es decir, si:
- \( f(a) \cdot f(b) < 0 \)
- entonces existe al menos un \( c \in (a, b) \) con \( f(c) = 0 \)
📌 Este teorema garantiza la existencia de una raíz, aunque no nos da su valor exacto. Es la base del método de bisección.
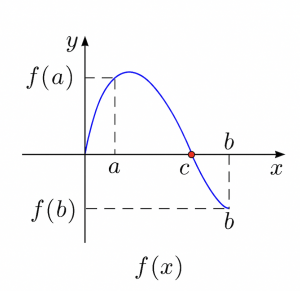
Teorema de los valores intermedios.
Si una función continua en un intervalo cerrado \( [a, b] \) toma dos valores \( f(a) \) y \( f(b) \), entonces toma todos los valores intermedios entre ellos.
Formalmente:
- Si \( f \) es continua en \( [a, b] \)
- y \( y_0 \) está entre \( f(a) \) y \( f(b) \)
- entonces existe al menos un \( c \in [a, b] \) tal que \( f(c) = y_0 \)
✅ Este teorema asegura que la función no da saltos y recorre todos los valores entre dos imágenes.
Teorema de Weierstrass.
Toda función continua en un intervalo cerrado y acotado alcanza un valor máximo y un valor mínimo absoluto.
Es decir, si \( f \) es continua en \( [a, b] \), entonces existen puntos \( x_{\text{min}}, x_{\text{max}} \in [a, b] \) tales que:
\[
f(x_{\text{min}}) \leq f(x) \leq f(x_{\text{max}}) \quad \text{para todo } x \in [a, b]
\]
🔍 Este teorema garantiza que una función continua alcanza sus extremos absolutos sobre intervalos cerrados, lo cual es clave en optimización.